这不是啥必题吗。但是为啥我场上也成啥必了呢。打表秒了全世界。
看到消 显然把 当作 , 当作 ,变为一个括号串。进一步的将括号串看作折线,不停的消去峰,那么最后剩下的折线就是一个 V 形。两个折线剩下的 V 形相同,也就相当于它们的最低点以及终点相同。将一个串翻转相当于把其对应折线旋转 ,于是我们可以导出一个折线合法的充要条件为下图中 :
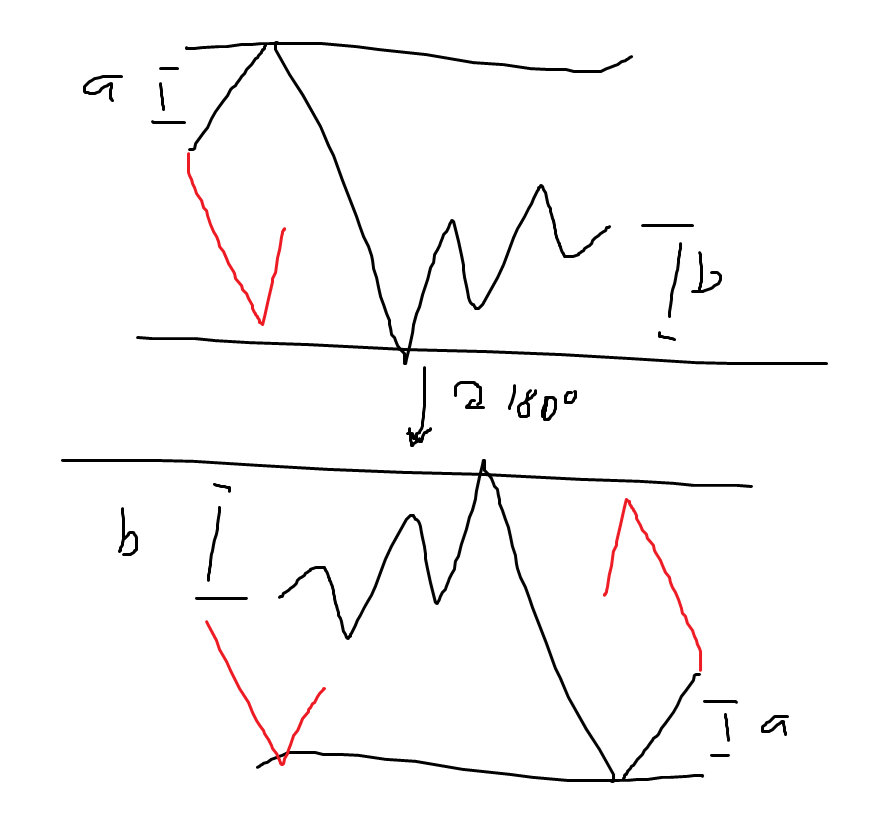
那么我们设 表示从 每次向右上或右下走一步,走到 且过程中 坐标最小值恰为 ,最大值恰为 的方案数,则要求的答案即为:
我们设 ,感觉上 可以 求。这里直接上一些手法来逃课数学推导,根据翻折容斥的过程,有系数 满足 。写一个 的暴力翻折容斥可以打表出系数 。通过简单观察可以发现 的规律,且 中只有 个位置不为 。这是 的表,这是 的表。
但是场上犯了一个非常蠢的错误就是我打的表是错的,对着错的表找了一个小时的规律,然后一直以为是规律不对,结束后才发现是表不对。
发现规律后可以根据规律写出 E1 的代码:
int tp = n & 1 ? 1 : 2;
ans = Pmod(2 * C(n, n + tp >> 1));
for (int k = tp;k <= n;k += 2){
for (int i = k * 3;i <= n;i += k * 2) add(ans, mod - 2ll * k * C(n, n + i >> 1) % mod);
for (int i = k * 3 + 2;i <= n;i += k * 2 + 2) add(ans, (k + 1ll) * 2 * C(n, n + i >> 1) % mod);
for (int i = k * 3 + 4;i <= n;i += k * 2 + 2) add(ans, (k + 1ll) * 2 * C(n, n + i >> 1) % mod);
for (int i = k * 3 + 6;i <= n;i += k * 2 + 4) add(ans, mod - (k + 2ll) * 2 * C(n, n + i >> 1) % mod);
}
时间复杂度为 。
然后这个东西可以直接无脑的改成 E2。具体来说,我们令 ,那么如果能算出 ,最终答案就是 。然后我们一一考虑上面的四种对 的贡献。拿第一种举例:
- 能对 带来 的贡献,当且仅当 ,也就是 。将 改写为 的形式,其中 均为正整数,那么我们要求的就是 ,这个只需要预处理出 即可 计算。
剩下的三个贡献条件分别为 ,,,推导过程在这里省略。可以发现这些都是类似的形式,也都是只需要预处理出 即可。
我们线性筛预处理出 即可单次 回答询问,于是我们就做完了。下面是代码:
inline int calc(int x){int p = x & -x;return 1ll * (ds[x / p] - x / p + mod) * p % mod;}
// ...
scanf("%d", &n);
int tp = n & 1 ? 1 : 2;
ans = Pmod(2 * C(n, n + tp >> 1));
for (int i = n + 2 >> 1, now;i <= n;i ++){now = 0;
add(now, mod - 4ll * calc(i * 2 - n) % mod);
add(now, Pmod(2 * calc(i * 2 - n + 1)));
if (i * 2 - n + 1 & 1) add(now, mod - 2);
if (i * 2 > n + 3){
add(now, Pmod(2 * calc(i * 2 - n - 1)));
if (i * 2 - n - 1 & 1) add(now, mod - 2);
}
if (i * 2 - n & 1){
if (i * 2 > n + 2) add(now, 2);
}
else if (i * 2 - n >> 1 & 1){
if (i * 2 > n + 5) add(now, 4);
}add(ans, 1ll * C(n, i) * now % mod);
}