菜王的 blog

先不考虑结束在 $(x, y)$ 的限制，考虑刻画合法路径的形态。可以发现，路径一定是类似以下的形式：

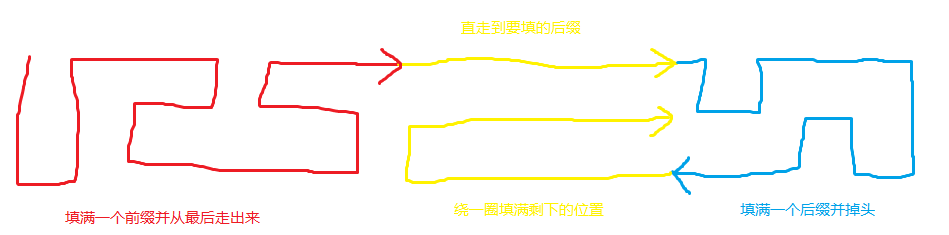
黄色段的情况是基本固定的，所以我们先考虑红色段和蓝色段的方案数。

红色段一定是许多“S”型拐弯拼在一起的，就像这样：

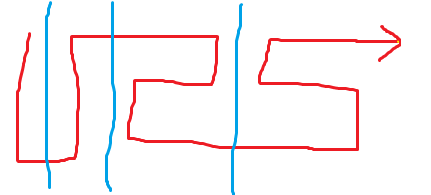
考虑设 $f_{i, 0 / 1}$ 表示填满长度为 $i$ 的前缀并结束于 $(1, i)$ 或 $(3, i)$ 的方案数，转移考虑每次延长最后一个拐弯，或者 新增一个新的拐弯，可以推出转移方程：$f_{0, 0} = 1, f_{1, 1} = 1, f_{i, 0} = f_{i, 1} = f_{i - 1, 0} + f_{i - 1, 1}$。当然你也可以推出 $f_{i, 0} = f_{i, 1} = 2^{i - 2} (i > 1)$。

蓝色段一定是许多“拱形”拼在一起的，就像这样：

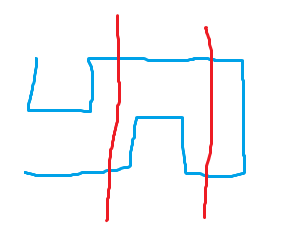
每一段拱形长度都是 $2$，要么第一列往下拱，要么第三列往上拱。设 $g_i$ 表示从左上进入，左下回来并填满一个长度为 $i$ 的后缀的方案数，则 $g_i$ 显然等于 $(i \bmod 2) \times 2^{\lfloor{\frac i2}\rfloor}$（即 $i$ 是偶数时不存在合法方案）。

考虑 $(x, y)$ 也是简单的，大概分类讨论一下：

1. 先把 $n < 3$ 的情况判掉。
2. $x = 2$ 的情况，一定是和第一张图一样的情况，前缀长度任意，后缀长度固定为 $n - y$，方案数为 $g_{n - y}\sum_{l = 0}^{y - 1} (f_{l, 0} + f_{l, 1})$。
3. $x = 1, 3$ 的情况是相似的，一起讨论：
   1. 先把 $y = n$ 的情况判掉，答案显然为 $f_{n, [x = 1]}$。
   2. 接下来枚举不存在黄色部分的方案数。方案数显然为 $f_{y - 1, [x = 1]}g_{n - y + 1}$。
   3. 如果黄色部分存在，则长度至少为 $3$。前缀长度任意，后缀长度固定为 $n - y - 1$，方案数为 $g_{n - y - 1}\sum_{l = 0}^{y - 2} f_{l, [x = 1]}$。

预处理出 $f, g$ 以及前缀和即可做到 $\mathcal O(1)$ 查询，当然也可以都化简成 $2^k$ 的形式，可做到无需预处理并 $\mathcal O(\log n)$ 查询，但是本题对时间复杂度要求是 $\mathcal O(n + T)$。