菜王的 blog

看出了双射但是不会优化了，哦不。双射好像和官方题解根本不一样，但是最后的式子是一样的。

以下令 $n = N - 1$，点的编号为 $0$ 到 $n$。那么我们对 $fa_i$（$1 \le i \le n$）的要求就是 $0 \le fa_i < i$ 且 $fa_{i - 1} \le fa_i$。那么我们可以将 $fa$ 序列看作一条 $(0, 0)$ 到 $(n, n)$ 且不越过 $y = x$ 的折线，而 $fa_i$ 即为 $x$ 坐标从 $i - 1$ 增加到 $i$ 时的 $y$ 坐标。

那么一次 $u \to fa_u$ 的操作就相当于从点 $u$（下文均将 $(x, x)$ 简化为点 $x$）向下走直到碰到折线，再向左走直到走回 $y = x$ 上，就走到了点 $fa_u$。我们令 $\mathrm{LCA}(n - 1, n) = p$，那么点 $n - 1$ 与点 $n$ 第一次在 $y = x$ 上相遇的位置即为点 $p$。

下面是一棵 $n = 8, d = 4, fa = (0, 0, 1, 3, 3, 3, 5, 6)$ 的树对应的折线：

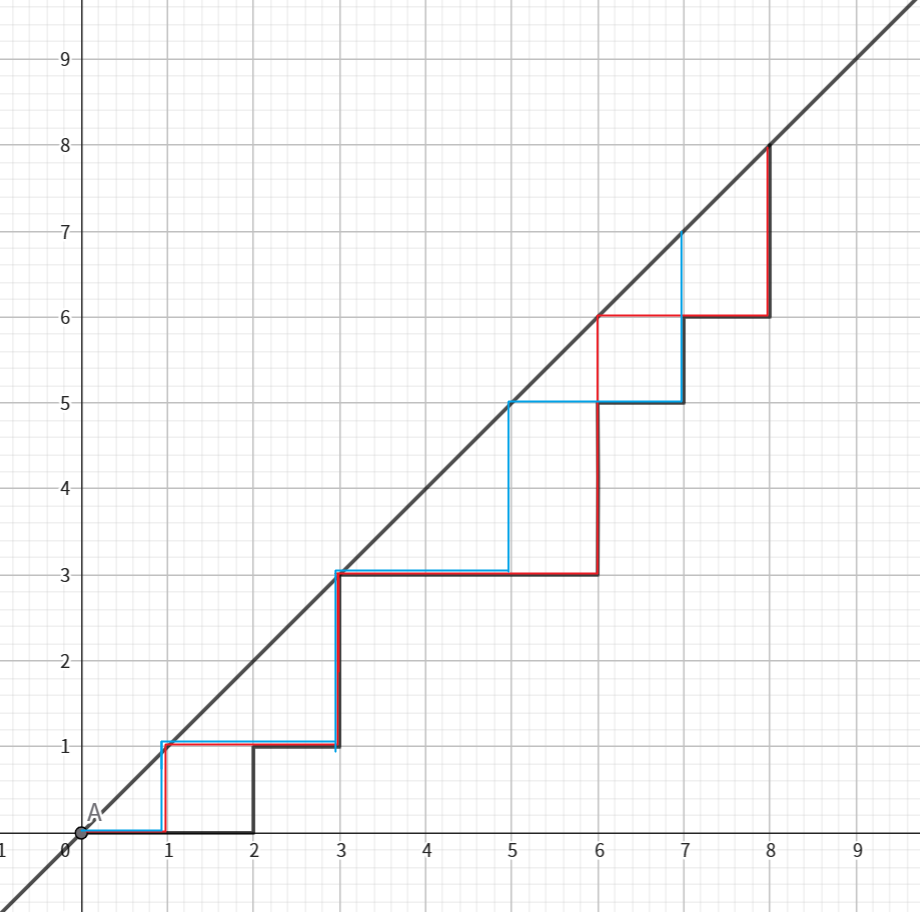
直接刻画还是比较困难，我们转而枚举红线和蓝线的形态，再算出合法的黑线数量。设点 $a_0, a_1, a_2, \dots, a_k$（$k \ge d$）为对角线上至少被红线和蓝线其中之一穿过的点，其中 $a_0 > a_1 > \cdots > a_k$，$a_0 = n, a_1 = n - 1$。那么红线会经过点 $a_0, a_2, a_4, \dots, a_d, a_{d + 1}, a_{d + 2}, \dots, a_k$，蓝线会经过 $a_1, a_3, a_5, \dots, a_d, a_{d + 1}, a_{d + 2}, \dots, a_k$。对黑线的要求就是，红线和蓝线的每个 J 型拐角下面都要被托住，相当于黑线必须过这些点：

• $(a_{i - 2}, a_i - 1), (a_{i - 2}, a_i)$（$2 \le i \le d$）；
• $(a_{i - 1}, a_i - 1), (a_{i - 1}, a_i)$（$\max(d, 1) \le i \le k$）；

这些限制显然不弱于不越过对角线的限制，所以我们忽略它。那么设 $b_i = a_{i - 1} - a_i$，则黑线的方案数为：

$\prod_{i = 3}^d \binom{b_i + b_{i - 2} - 1}{b_i} \prod_{i = d + 1}^k \binom{b_i + b_{i - 1} - 1}{b_i}$

由于 $b_1 = 1$，式子可以改为：

$\prod_{i = 4}^d \binom{b_i + b_{i - 2} - 1}{b_i} \prod_{i = d + 1}^k \binom{b_i + b_{i - 1} - 1}{b_i}$

设所有长度为 $m$，总和为 $n$ 的正整数序列 $a'$ 的 $\prod_{i = 2}^m \binom{a'_i + a'_{i - 1} - 1}{a'_i}$ 之和为 $F(m, n)$，那么答案式子可以写成这样：

$\sum_{x = 0}^{n - 1} F((d - 1) / 2, x) \sum_{k = d} F(k - (d - 1) / 2, n - 1 - x)$

考虑计算。考虑 $\prod_{i = 2}^m \binom{a'_i + a'_{i - 1} - 1}{a'_i}$ 的组合意义实际上是长度为 $n$，值域为 $m$，$i$ 恰好出现 $a'_i$ 次，且 $c_i \le c_{i - 1} + 1$ 的正整数序列 $c$ 的个数。证明是简单的，考虑从小到大插入元素，每个 $i - 1$ 之后都会紧跟着连续的若干个 $i$。我们设 $G(m, n) = \sum_{i = 1}^{m - 1} F(i, n)$，那么 $G(m, n)$ 即为所有长度为 $n$，值域为 $m - 1$ 且 $c_i \le c_{i - 1} + 1$ 的正整数序列 $c$ 的个数，则 $F(m, n) = G(m + 1, n) - G(m, n)$。

考虑计算 $G$。考虑 $c$ 序列的生成过程：维护一个初始为 $0$ 的变量 $x$，每次可以选择以下两种操作之一：

• $x \gets x + 1$ 并向 $c$ 序列末尾加入 $x$。
• $x \gets x - 1$。

最后 $x$ 的值需要变回 $0$。显然，在满足任何时候都有 $0 \le x < m$ 的基础上操作 $2n$ 次和一个合法 $c$ 序列构成双射。那么 $G(n, m)$ 即为 $(0, 0)$ 走到 $(n, n)$ 且不经过 $y = x + 1$ 与 $y = x - m$ 两条直线的方案数，翻折容斥即可。

使用 $G$ 重写答案式子：

$\sum_{x = 0}^{n - 1} (G((d + 1) / 2, x) - G((d - 1) / 2, x))(G(n, n - 1 - x) - G(d / 2, n - 1 - x))$

至此可以 $O(n^2 \ln n)$ 计算，但是没有什么用。考虑优化。

发现我们需要算的东西是形如 $\sum_{i = 0}^n G(k1, i) G(k2, n - i)$ 的。这又可以转化为计算 $\mathcal{O}(\frac{n^2}{k1k2})$ 个 $\sum_{i = 0}^n \binom{2i}{i + p} \binom{2n - 2i}{n - i + q}$ 状物，而它的组合意义是 $(0, 0)$ 走到 $(n - p - q, n + p + q)$ 的所有路径与直线 $y = x + p$ 的相交次数之和。根据这篇文章，这是 $\sum_{i = m}^{2n + 1} \binom{2n + 1}i$，一个组合数后缀和。$\mathcal{O}(n)$ 预处理出组合数后缀和 $g_i$ 后答案即为 $\sum f_ig_i$。

分情况讨论。对于 $k2 = n$ 的两种情况，$\mathcal{O}(\frac{n^2}{k1k2}) = \mathcal{O}(\frac nd)$，可以暴力算。对于 $k1 = k2$ 的情况，由于上式中的 $p, q$ 分别可以表示为 $b + k1 x, b + k2 x$ 的形式，而其中 $b$ 只有 $\mathcal{O}(1)$ 种取值，所以 $f_i$ 只有 $\mathcal{O}(\frac nd)$ 个位置有值。$k2 = k1 + 1$ 的情况，它没有前一种情况的性质，然后想了很久不会算。看了官方题解，可以将折线看作括号序列后有答案等于 $\text{(} + G(i, k1) + \text{)} + G(n - 1 - i, k2)$，也就是 $G(n, k2)$，可以 $\mathcal{O}(\frac nd)$ 算。

于是最终时间复杂度为调和级数 $\mathcal{O}(n \ln n)$。代码。