菜王的 blog

首先考虑最小化逆序对数量。容易发现，对于一对 $(i, j)$，它们是否产生逆序对是由 $p_i, p_j$ 中更大的那个取正还是取负来决定的，与更小的那个无关。于是令 $L_i = \sum_{j < i} [p_j < p_i]$，$R_i = \sum_{j > i} [p_j < p_i]$，则答案为 $\sum \min(L_i, R_i)$。假设我们现在正在计算 $ans_x$，即 $p_k = x$ 的答案。

首先考虑 $i = k$ 时的贡献。枚举 $[1, x - 1]$ 里的数的分布情况，可以列出式子：

$(x - 1)!(n - x)! \sum_{i + j = x - 1} \binom{k - 1}i \binom{n - k}j \min(i, j)$

接下来考虑 $i \ne k$ 时的贡献。我们采用这样的想法：首先将 $p_k$ 从序列中移除，算出贡献之后再将 $p_k$ 插回原位置并且修正贡献。

移除 $p_k$ 之后的贡献相当于没有固定任何位置的 $n' = n - 1$ 的问题，我们对于每一个 $i$ 求出 $\min(L_i, R_i)$ 之和再相加：

$\sum_{i = 1}^{n - 1} \binom{n - 1}i (i - 1)!(n - 1 - i)! \sum_{j = 1}^i \min(j - 1, i - j)\\ \sum_{j = 1}^i \min(j - 1, i - j) = \left\lfloor\frac i2\right\rfloor \left\lfloor\frac{i - 1}2\right\rfloor$

这可以 $\mathcal{O}(n)$ 计算。把这个式子计入每个 $ans_x$。

考虑修正贡献。考虑当我们把 $p_k = x$ 插回原序列对一个满足 $p_l = y > x$ 的位置 $l$ 的 $\min(L_l, R_l)$ 的影响。影响显然是，如果 $k < l$ 且 $L_l < R_l$，或 $k > l$ 且 $R_l < L_l$，插入之后的 $\min(L_l, R_l)$ 会比原来增加 $1$。

枚举 $k$ 左右两边分别填了 $i, j$ 个 $\le y$ 的数，则 $y = i + j + 1$。如果 $k < l$，那么 $y$ 在这 $y$ 个数中位置的排名应该 $< \frac{y + 1}2$；否则应该 $> \frac{y + 1}2$。可以得到确定 $y$ 的位置的方案有 $\left\lfloor\frac{|i - j|}2\right\rfloor$ 种。

可以发现列出的式子和 $x$ 是没有关系的，只要求 $y > x$。列出式子：

$(y - 2)!(n - y)! \sum_{i + j = y - 1} \left\lfloor\frac{|i - j|}2\right\rfloor \binom{k - 1}i \binom{n - k}j$

我们对每个 $y$ 求出这个，然后把它贡献到 $x < y$ 的 $ans_x$ 上。

$|i - j|$ 可以写成 $i + j - 2\min(i, j)$。那么 $\left\lfloor\frac{|i - j|}2\right\rfloor$ 可以写成 $\left\lfloor\frac{i + j}2\right\rfloor - \min(i, j)$。前者显然只和 $i + j$ 有关，可以提到求和外面去。

现在就只需要对于每个 $x$ 求出下面两个东西：

$\sum_{i + j = x} \binom{k - 1}i \binom{n - k}j\\ \sum_{i + j = x} \binom{k - 1}i \binom{n - k}j \min(i, j)\\$

前者显然是 $\binom{n - 1}x$，不作解释。对于后者，我们可以直接钦定 $i, j$ 的大小关系并且做一个分治 NTT 来解决，时间复杂度为 $\mathcal{O}(n \log^2 n)$。代码。

然而我们有一个更高妙的做法可以做到线性。以下思路来自这篇题解。

以下令 $A = k - 1, B = n - k$。那么我们需要对所有的 $i$ 求这个。

$\sum_{j = 0}^i \binom Aj \binom B{i - j} \min(j, i - j)\\$

直接暴力展开。

$\sum_{j = 0}^i \frac{A!B!}{j!(A - j)!(i - j)!(B - i + j)!} \min(j, i - j)\\$

一个很神奇的事情是，我们可以把分母里的阶乘重新配对。

$\frac{A!B!}{i!(A + B - i)!}\sum_{j = 0}^i \frac{i!(A + B - i)!}{j!(i - j)!(A - j)!(B - i + j)!} \min(j, i - j)\\ \frac{A!B!}{i!(A + B - i)!}\sum_{j = 0}^i \binom ij \binom{A + B - i}{A - j} \min(j, i - j)\\$

可以发现后面一部分式子的组合意义就是，所有从 $(0, 0)$ 到 $(A, B)$ 的路径与 $x + y = i$ 的交点的横纵坐标的 $\min$ 之和，记其为 $f(i)$。

考虑 $f(i) - f(i - 1)$ 的意义：对于一条路径，记它与 $x + y = i$ 的交点的横纵坐标的 $\min$ 为 $p(i)$，则 $p(i) - p(i - 1) \in \{0, 1\}$。$f(i) - f(i - 1)$ 统计的就是满足 $p(i) - p(i - 1) = 1$ 的路径条数。

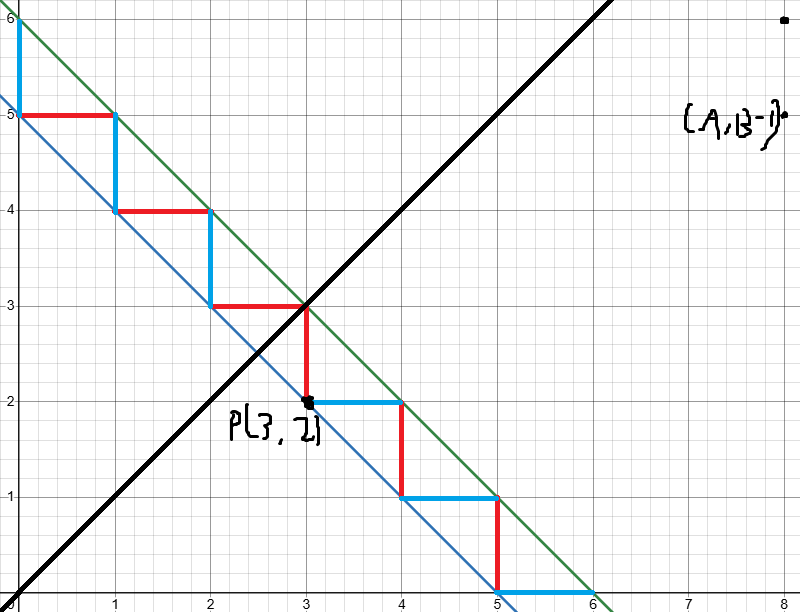
这张图是 $A = 8, B = 6, i = 6$ 的情况。显然每一条从 $(0, 0)$ 到 $(A, B)$ 的路径都会恰好经过图中一条红色或蓝色的线段。而我们需要统计的就是经过红色线段的路径。考虑分别统计经过对角线上方、下方的红色线段的路径条数，它们的流程是相同的，这里拿对角线下方来举例。

可以发现，经过对角线下方的红色线段的路径条数就是从 $(0, 0)$ 走到 $(A, B - 1)$ 且 $P(3, 2)$ 不在其上方（路径经过 $P$ 是允许的）的路径条数。这并不能直接 $\mathcal{O}(1)$ 计算，但是随着 $i$ 的增加，$P$ 每次只会移动到相邻的位置，这对方案数的影响可以 $\mathcal{O}(1)$ 计算。

做一个前缀和就可以 $\mathcal{O}(n)$ 求出所有 $f(i)$，于是我们就做完了。代码。